Matemática Tercero BGU Informatica y Marketing UED
lunes, 11 de enero de 2016
Ecuaciones Exponenciales y logaritmicas
En los enlaces podras descargar notas sobre Logaritmos y Exponenciales
lunes, 9 de noviembre de 2015
lunes, 21 de septiembre de 2015
Bases Álgebra 03
Factoreo
Factor Común
1. Se identifica el factor común
2. Se divide cada término del polinomio por el factor común
3. Se escribe el factor común y a continuación, dentro de un paréntesis, los cocientes hallados en el paso anterior (cada uno precedido de su respectivo signo)
1. 
2. 
3. 
4. 
Factor común por agrupación de términos
1. Se agrupan los términos convenientemente, utilizando paréntesis
2. Se saca factor común de cada uno de los paréntesis
3. Se realiza una segunda factorización (el factor común será, en este caso, el paréntesis.
1. 
2. 
Trinomio cuadrado perfecto
Una cantidad es un cuadrado perfecto cuando es el resultado del producto de dos factores iguales.
1. Se ordena el trinomio
2. Se extrae la raíz cuadrada del primer y tercer términos
3. Se halla el doble producto de las raíces obtenidas en el paso anterior
4. Si el producto hallado en el paso anterior es igual al segundo término del trinomio y si el primero y tercer términos tienen igual signo, se trata de un trinomio cuadrado perfecto y se Factorizar como tal.
5. Se escribe dentro de un paréntesis las raíces cuadradas del primer y tercer término, separadas por el signo del segundo término, y el paréntesis elevado al cuadrado.
1. 
2. 
Diferencia de cuadrados perfectos
1. Se extrae la raíz cuadrada al minuendo y al sustraendo
2. Se abren dos paréntesis
3. En el primer paréntesis se escribe la suma, y en el segundo la diferencia, de las raíces halladas en el paso 1.
1. 
Diferencia de cuadrados perfectos (caso especial)
1. Se extrae la raíz cuadrada al minuendo y al sustraendo
2. Se abren dos paréntesis
3. En el primer paréntesis se escribe la suma, y en el segundo la diferencia, de las raíces halladas en el paso 1.
4. Se reduce, si es el caso
1. 
2. 
Trinomio cuadrado perfecto y diferencia de cuadrados perfectos (combinación de estos dos casos)
1. Se identifica el trinomio cuadrado perfecto (o los ...)
2. Se factoriza el trinomio cuadrado perfecto
3. Se factoriza la diferencia de cuadrados resultante
4. Se reduce, si es el caso
1. 
2. 
Trinomio cuadrado perfecto por adición y sustracción
1. Se ordena el trinomio
2. Se extrae la raíz cuadrada del primer y tercer términos
3. Se halla el doble producto de las raíces halladas en el paso anterior
4. Se compara el resultado obtenido en el paso anterior con el segundo término del trinomio
5. Se suma o resta, según el caso, la cantidad necesaria para crear el segundo término del trinomio cuadrado perfecto
6. Se resta o se suma la misma cantidad que se sumo o resto en el paso anterior, para que el valor de la expresión no se altere
1. 
2. 
Trinomio cuadrado perfecto por adición y sustracción
Factorizar una suma de dos cuadrados
1. Se extrae la raíz cuadrada de ambos términos
2. Se halla el doble producto de las raíces halladas en el paso anterior
3. Se suma y se resta el producto hallado en el paso anterior
4. Se factoriza el trinomio cuadrado perfecto así formado
5. Se factoriza la diferencia de cuadrados
1. 
Trinomio de la forma 
1. Se ordena el trinomio
2. Se abren dos paréntesis, en cada uno de los cuales se escribirá un binomio
3. Se saca la raíz cuadrada del primer término del trinomio, esta raíz será el primer término de cada uno de los paréntesis
4. El signo que separe al binomio del primer paréntesis será el segundo signo del trinomio
5. Se aplica la "ley de los signos" al producto de los signos del segundo y tercer términos del trinomio; éste será el signo que separe el binomio del segundo paréntesis
6. Si los signos son iguales, se buscan dos números cuya suma sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
7. Si los signos son diferentes, se buscan dos números cuya diferencia sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
8. El mayor de los números hallados en uno de los pasos anteriores será el segundo término del primer paréntesis, el menor de los números será el segundo término del segundo paréntesis
9. Si el tercer término es un número muy grande se descompone en sus factores primos para facilitar la búsqueda de los números requeridos en los pasos 7 y 8
1. 
Casos especiales
1. 
2. 
Trinomio de la forma 
1. Se multiplica y divide el trinomio por el coeficiente del primer término, esto es por a
2. Se escribe el trinomio de una forma adecuada (de la forma x2 + bx+ c)
3. Se abren dos paréntesis, en cada uno de los cuales se escribirá un binomio
4. Se saca la raíz cuadrada del primer término del trinomio, esta raíz será el primer término de cada uno de los paréntesis
5. El signo que separe al binomio del primer paréntesis será el segundo signo del trinomio
6. Se aplica la "ley de los signos" al producto de los signos del segundo y tercer términos del trinomio; éste será el signo que separe el binomio del segundo paréntesis
7 Si los signos son iguales, se buscan dos números cuya suma sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
8 Si los signos son diferentes, se buscan dos números cuya diferencia sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
9. El mayor de los números hallados en uno de los pasos anteriores será el segundo término del primer paréntesis, el menor de los números será el segundo término del segundo paréntesis
10. Si el tercer término es un número muy grande se descompone en sus factores primos para facilitar la búsqueda de los números requeridos en los pasos 7 y 8
11. Se factorizan los paréntesis que tengan factor común
12. Se simplifica
1. 
2. 
Factorizar una expresión que es el cubo de un binomio
El desarrollo del cubo de un binomio es:
En esta clase de ejercicios se nos da una expresión como el miembro derecho de las
identidades anteriores, es decir un cuadrinomio; y debemos constatar si se trata de un
cubo perfecto de binomios (como los miembros izquierdos de las expresiones
anteriores); para lo cual debemos proceder:
1. Se ordena el cuadrinomio en forma descendente o ascendente respecto a una letra
2. Se extrae la raíz cúbica del primero y cuarto términos del cuadrinomio
3. Se observa si todos los signos son positivos o si se alternan positivo‐negativopositivo‐negativo
4. Se triplica el cuadrado de la raíz cúbica del primer término por la raíz cúbica del
cuarto término y se compara con el segundo término del cuadrinomio dado
5. Se triplica la raíz cúbica del primer término por el cuadrado de la raíz cúbica del cuarto término y se compara con el tercer término del cuadrinomio dado
6. Si las dos comparaciones hechas en los pasos 4 y 5 son positivas, se trata del desarrollo del cubo de un binomio y se factoriza como tal: dentro de un paréntesis se escriben las raíces cúbicas del primero y cuarto términos del cuadrinomio y separadas por el signo más o por el signo menos, según el caso; y se eleva al cubo el paréntesis
7. Si las dos comparaciones hechas en los pasos 4 y 5 son negativas, no se trata del desarrollo del cubo de un binomio y no se puede factorizar como tal
1. 
2. 
Suma o diferencia de cubos perfectos
1. Se abren dos paréntesis
2. En el primer paréntesis se escribe la suma o la diferencia, según el caso, de las raíces cúbicas de los dos términos
3. En el segundo paréntesis se escribe el cuadrado de la primera raíz, menos (si es una suma de cubos) o más (si es una diferencia de cubos) el producto de la primera raíz por la segunda, mas el cuadrado de la segunda raíz
1. 
2. 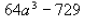
Casos especiales
1. 
Suscribirse a:
Entradas (Atom)




























